TextRank摘要算法实现原理

Posted on | In | | Heat: ℃
Words count in article: 2,154 words | Reading time ≈ 10 min

所谓自动摘要，就是从文章中自动抽取关键句。何谓关键句？人类的理解是能够概括文章中心的句子，机器的理解只能模拟人类的理解，即拟定一个权重的评分标准，给每个句子打分，之后给出排名靠前的几个句子。

相似度计算

TextRank的打分思想依然是从PageRank的迭代思想衍生过来的，如下公式所示：

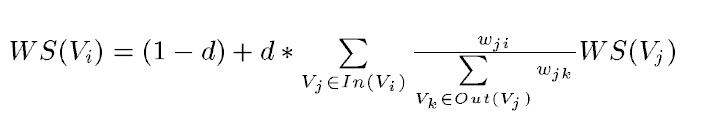
创新扩散曲线

等式左边表示一个句子的权重（WS是weight_sum的缩写），右侧的求和表示每个相邻句子对本句子的贡献程度。与提取关键字的时候不同，一般认为全部句子都是相邻的，不再提取窗口。

求和的分子wji表示两个句子的相似程度，分母又是一个weight_sum，而WS(Vj)代表上次迭代j的权重。整个公式是一个迭代的过程。

相似度计算

而相似程度Wij的计算，推荐使用BM25

BM25算法，通常用来作搜索相关性评分。一句话概况其主要思想：对Query进行语素解析，生成语素qi；然后，对于每个搜索结果D，计算每个语素qi与D的相关性得分，最后，将qi相对于D的相关性得分进行加权求和，从而得到Query与D的相关性得分。

算法连接

测试用例

1
2
3
4
5
6
7
8
9
算法可大致分为基本算法、数据结构的算法、数论算法、计算几何的算法、图的算法、动态规划以及数值分析、加密算法、排序算法、检索算法、随机化算法、并行算法、厄米变形模型、随机森林算法。

算法可以宽泛的分为三类，

一，有限的确定性算法，这类算法在有限的一段时间内终止。他们可能要花很长时间来执行指定的任务，但仍将在一定的时间内终止。这类算法得出的结果常取决于输入值。

二，有限的非确定算法，这类算法在有限的时间内终止。然而，对于一个（或一些）给定的数值，算法的结果并不是唯一的或确定的。

三，无限的算法，是那些由于没有定义终止定义条件，或定义的条件无法由输入的数据满足而不终止运行的算法。通常，无限算法的产生是由于未能确定的定义终止条件。

断句

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
算法可大致分为基本算法、数据结构的算法、数论算法、计算几何的算法、图的算法、动态规划以及数值分析、加密算法、排序算法、检索算法、随机化算法、并行算法、厄米变形模型、随机森林算法
算法可以宽泛的分为三类
一
有限的确定性算法
这类算法在有限的一段时间内终止
他们可能要花很长时间来执行指定的任务
但仍将在一定的时间内终止
这类算法得出的结果常取决于输入值
二
有限的非确定算法
这类算法在有限的时间内终止
然而
对于一个（或一些）给定的数值
算法的结果并不是唯一的或确定的
三
无限的算法
是那些由于没有定义终止定义条件
或定义的条件无法由输入的数据满足而不终止运行的算法
通常
无限算法的产生是由于未能确定的定义终止条件

分词并过滤停用词

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
[算法, 大致, 分, 基本, 算法, 数据, 结构, 算法, 数论, 算法, 计算, 几何, 算法, 图, 算法, 动态, 规划, 数值, 分析, 加密, 算法, 排序, 算法, 检索, 算法, 随机, 化, 算法, 并行, 算法, 厄, 米, 变形, 模型, 随机, 森林, 算法]
[算法, 宽泛, 分为, 三类]
[]
[有限, 确定性, 算法]
[类, 算法, 有限, 一段, 时间, 终止]
[可能, 花, 长, 时间, 执行, 指定, 任务]
[一定, 时间, 终止]
[类, 算法, 得出, 常, 取决, 输入, 值]
[二]
[有限, 非, 确定, 算法]
[类, 算法, 有限, 时间, 终止]
[]
[一个, 定, 数值]
[算法, 唯一, 确定]
[三]
[无限, 算法]
[没有, 定义, 终止, 定义, 条件]
[定义, 条件, 无法, 输入, 数据, 满足, 终止, 运行, 算法]
[通常]
[无限, 算法, 产生, 未, 确定, 定义, 终止, 条件]

计算BM25相关矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
[15.176530737482341, -2.604484103028904, 0.0, -2.8740684265166565, -2.1930693258940175, 0.0, 0.0, -2.0325355810136103, 0.0, -2.604484103028904, -2.3811362523642052, 0.0, 2.509043358515279, -2.8740684265166565, 0.0, -3.2059044218809922, 0.0, -0.22517864251663589, 0.0, -1.8939010965185548]
[-0.2864022115473306, 8.52437122545896, 0.0, -0.23950570220972142, -0.18275577715783484, 0.0, 0.0, -0.1693779650844675, 0.0, -0.21704034191907534, -0.19842802103035043, 0.0, 0.0, -0.23950570220972142, 0.0, -0.267158701823416, 0.0, -0.1477475757866994, 0.0, -0.15782509137654627]
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]
[-0.2864022115473306, -0.21704034191907534, 0.0, 4.604672851367114, 1.060086217315166, 0.0, 0.0, -0.1693779650844675, 0.0, 1.2589559610532894, 1.1509940396671094, 0.0, 0.0, -0.23950570220972142, 0.0, -0.267158701823416, 0.0, -0.1477475757866994, 0.0, -0.15782509137654627]
[-0.2864022115473306, -0.21704034191907534, 0.0, 1.3892676764009562, 7.063472116341414, 1.1518653539666401, 2.634590118176154, 1.2574519044179069, 0.0, 1.2589559610532894, 5.005270773642655, 0.0, 0.0, -0.23950570220972142, 0.0, -0.267158701823416, 0.8333088661764476, 0.4727261064071153, 0.0, 0.504969645305668]
[0.0, 0.0, 0.0, 0.0, 1.2428419944730007, 14.795434933306574, 1.6287733786106775, 0.0, 0.0, 0.0, 1.3494220606974598, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0, 2.010334451736872, 1.1518653539666401, 5.849995293142312, 0.0, 0.0, 0.0, 2.1827309268739077, 0.0, 0.0, 0.0, 0.0, 0.0, 0.8333088661764476, 0.6204736821938147, 0.0, 0.6627947366822143]
[-0.2864022115473306, -0.21704034191907534, 0.0, -0.23950570220972142, 1.356767982871274, 0.0, 0.0, 12.127555522767913, 0.0, -0.21704034191907534, 1.4731177860712878, 0.0, 0.0, -0.23950570220972142, 0.0, -0.267158701823416, 0.0, 1.4000446911370572, 0.0, -0.15782509137654627]
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 4.054814792796337, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]
[-0.2864022115473306, -0.21704034191907534, 0.0, 1.3892676764009562, 1.060086217315166, 0.0, 0.0, -0.1693779650844675, 0.0, 6.001094704342757, 1.1509940396671094, 0.0, 0.0, 1.7780760396570634, 0.0, -0.267158701823416, 0.0, -0.1477475757866994, 0.0, 1.1716840594784514]
[-0.2864022115473306, -0.21704034191907534, 0.0, 1.3892676764009562, 4.609944429081147, 1.1518653539666401, 2.634590118176154, 1.2574519044179069, 0.0, 1.2589559610532894, 5.005270773642655, 0.0, 0.0, -0.23950570220972142, 0.0, -0.267158701823416, 0.8333088661764476, 0.4727261064071153, 0.0, 0.504969645305668]
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]
[0.5551884973225691, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 8.939853708447595, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]
[-0.2864022115473306, -0.21704034191907534, 0.0, -0.23950570220972142, -0.18275577715783484, 0.0, 0.0, -0.1693779650844675, 0.0, 1.611294545577714, -0.19842802103035043, 0.0, 0.0, 4.9934812146232215, 0.0, -0.267158701823416, 0.0, -0.1477475757866994, 0.0, 1.1716840594784514]
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 4.054814792796337, 0.0, 0.0, 0.0, 0.0, 0.0]
[-0.2864022115473306, -0.21704034191907534, 0.0, -0.23950570220972142, -0.18275577715783484, 0.0, 0.0, -0.1693779650844675, 0.0, -0.21704034191907534, -0.19842802103035043, 0.0, 0.0, -0.23950570220972142, 0.0, 2.531575358765468, 0.0, -0.1477475757866994, 0.0, 1.4955384555950606]
[0.0, 0.0, 0.0, 0.0, 0.7674924572638717, 0.0, 1.0058167395654765, 0.0, 0.0, 0.0, 0.8333088661764476, 0.0, 0.0, 0.0, 0.0, 0.0, 9.892547495751218, 4.354323965031352, 0.0, 4.651322189247207]
[0.26878628577523855, -0.21704034191907534, 0.0, -0.23950570220972142, 0.5847366801060369, 0.0, 1.0058167395654765, 1.6050126003722507, 0.0, -0.21704034191907534, 0.6348808451460972, 0.0, 0.0, -0.23950570220972142, 0.0, -0.267158701823416, 4.866735958438866, 12.008153881124132, 0.0, 3.1639879470156633]
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 4.054814792796337, 0.0]
[-0.2864022115473306, -0.21704034191907534, 0.0, -0.23950570220972142, 0.5847366801060369, 0.0, 1.0058167395654765, -0.1693779650844675, 0.0, 1.611294545577714, 0.6348808451460972, 0.0, 0.0, 1.7780760396570634, 0.0, 2.531575358765468, 4.866735958438866, 2.9619596282988065, 0.0, 10.38451854500608]

迭代投票

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
for (int _ = 0; _ < max_iter; ++_)
{
    double[] m = new double[D];
    double max_diff = 0;
    for (int i = 0; i < D; ++i)
    {
        m[i] = 1 - d;
        for (int j = 0; j < D; ++j)
        {
            if (j == i || weight_sum[j] == 0) continue;
            m[i] += (d * weight[j][i] / weight_sum[j] * vertex[j]);
        }
        double diff = Math.abs(m[i] - vertex[i]);
        if (diff > max_diff)
        {
            max_diff = diff;
        }
    }
    vertex = m;
    if (max_diff <= min_diff) break;
}

输出排序结果

  • 这类算法在有限的时间内终止
  • 这类算法在有限的一段时间内终止
  • 无限算法的产生是由于未能确定的定义终止条件

效果还可以。

-------------本文结束感谢您的阅读-------------